 Math is everywhere! I always get excited when I see math used in tv shows, movies, and articles. I typically use these artifacts as class openers to introduce a topic or as a closer to make drive the point home. Now, I will say that some of the examples shown show math in a silly or intimidating way. This is very representative of society's view of mathematics: a difficult complex science that cannot be mastered. I will explain this for each. Sherlock Homes: A Game of Shadows (Pascal's Triangle) This came over during the Holiday Break of the 2011-2012 school year. I reluctantly saw it with a friend (ended up loving it) and was excited to see Pascal's Triangle on the board of the evil dude as a ciphering code for his notebook with his plans to take over the world. I had covered Pascal's Triangles with my 9th graders in the fall and was curious to see if any of them noticed it (the movie did zoom in on it and I think it is the scene shown in the picture.) They did! The link above leads to a publication which goes way more into detail on the math used. I just used is as a "you actually learn stuff in this class that you will see in the media." Now, this is an example of math being used by a super genius trying to ruin the world so it may not have a great vibe on the math but Sherlock had to use math knowledge to save the world so that is good right? I told my students I was showing them math that they could use to take over the world or save the world. Go On (Fibonacci Sequence) Season 1 Episode 12 This was my first summer completely off so I watched some television shows (thank you Netflix/Hulu) that I probably would of not seen if not for my restlessness. Matthew Perry's character in Go On does a sports segment with some famous sports guy who decides to change the focus of his show from sports to philosophy topics. He asks Matthew about his opinion on Fibonacci and Matthew is confused and lists off the first sequence he can think of...911. It is another not so positive jab at math but at least 50% of the people in the discussion know about Fibonacci. I am still in debate if I will use this clip in my classes this year. Raising Hope (Area of a Circle) Season 2 Episode 11 Alright, it is hard to show math being portrayed in modern media. This would actually be an interesting topic for a research paper or article (maybe that will be a goal of mine this semester). Here is another poke at mathematics were the only person who knows anything about calculating the area of a circle is the memory challenged grandmother. I know I teach this topic in Pre-Algebra this school year so it would fit in easily but once again I am debating on the message it sends about the inaccessibility of math.
6 Comments
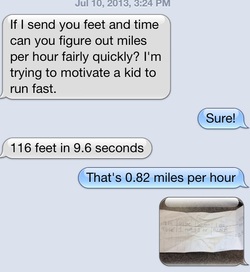 I love solving problems. There is something very satisfying to me about figuring out a solution. This is amplified when a friend asks me a math question and when the answer has real world applications. This past Wednesday, a dear friend who is pericardiac physical therapist sent me the following text (shown to the left) asking me to convert feet/seconds to miles/hour. I was thrilled to but I was shopping with no pen and only had receipts for paper. I paused shopping and worked out the problem (thank you dimensional analysis) after borrowing a pen from a cashier. I took a picture of my work and sent her the solution. Excited to teach dimensional analysis this year and use this as an example. ***Correction update*** Whoops. The conversion is actually 8.2 miles per hour. I forgot to type in a '0' in phone calculator and messed up the decimal. Thanks for pointing this out NS!  Yes. The answer is yes you can study mathematics. There is apparently a rumor going around telling students that math cannot be studied. This is a lie. Run from the darkness. The issue is students need to learn how to study math. This is where I, as the teacher, come in to hopefully fly in to save the day. Here is the list of ways I personally have studied math and instruct my students to do so. Cheat Sheet (See photo to the left) Start reviewing notes, power-points, textbook, or whatever form the material being tested was presented on and on a blank sheet of paper write out problems, equations, formulas, and helpful hints on the material you do not 100% understand. This is your "cheat sheet." Writing the topics you do not feel comfortable with allow your brain to process the material from start to finish and you get to "feel" how the topic is worked out. When I was a student, I would do this multiple times on separate days before a test. Your cheat sheet should get shorter and shorter the more times you complete this exercise. On the last night my sheet would short so I had less material to work through. I like this method because it works for all subjects and it a great to hold onto for use in studying for finals. The picture shown is one of my students "cheat sheets" that he created for his final test (that I did let students use). This does take time but with more repetitions on the same topic the quicker the process will go. Flashcards This is a fabulous tool to use with units where there is vocabulary, properties, and formulas that will tested. Old-school using lined index cards and new-school sites like quizzlet are great tools to use while studying. I prefer old-school paper index cards because I learn best when I write the material down (my love of cheat sheets is explained) but I have seen more students lean more towards quizzlet-like sites. The advantage of quizzlet is that you can share your creating with others. YouTube Videos I have written of my love for YouTube as a teaching method I use in class so it should be not surprise that I am using it again. I believe that YouTube gets rid of the excuse for students that they do not understand the material on test day (even if they were absent.) It has EVERY TOPIC YOU CAN IMAGINE on it. Simply type to topic in the search bar and 1,000s of videos will appear. I recommend starting with the first one that pops up. You do not like the person on the video you say? pick another one! Extra Practice Problems (the whole problem, on a clean sheet of paper without referring to the worked out example) As a coach, I know what my athletes do during practice is a direct implication on how they will preform on game/match/race/meet day. I also know that an athlete does not become an expert by watching me practicing the stroke/running technique but rather by practicing the technique. The same is true with math. Working out extra problems from start to finish does help. I find that students give into the lie that if they understand a problem by watching me going through it problem, hearing my explantation for it, and seeing my work on the board for it that they understand that topic. NOT REALLY TRUE. A student really knows the topic if they can work out a problem from start to finish without assistance. This is why I give my students a study guide/practice test for each test. Bottom line...to study math you have to take time to study the math. You will not be able to magically get all topics, it will take work. Take the time to figure out what works. There are plenty more ideas, these are just the top Work with different strategies to see what works. One method may work for one topic but not for the next. How do you study mathematics?  While I am on Pinterest, I notice some funny math posters/ideas/the thing where you add a saying to a picture. Here are some of my favorites. These are great to look at for a quick laugh and I have used some in lessons as an introduction or ending. The pizza one shown first on the slide show is a new one for me and I will be using it for volume this upcoming year. Have fun and laugh a little.  I spent Memorial Day Weekend on the beaches of South Walton County. It was amazing. The weather was incredible. The water was perfect. The condo I stayed in had a keypad in which we were given a unique code. While talking to one of my friends, she became worried about the code being easy to figure out. No fear, I told her, math can put your worry to rest. The code was 6 digits. So using the multiplication counting principle, there are 10 * 10 * 10 * 10 * 10 * 10 = 10 ^ 6 = 1,000,000 different codes. The odds of someone randomly punching in out code was 1/1,000,000 or simple said, one in a million. The probability showed that we were safe. Even if someone had the first three digits of the code that still left a 1/(10 * 10 * 10) or 1 in 10,000 chance of getting the last three digits correctly. This led to my friend rolling her eyes at me. There is also a fabulous book entitled "One in a Million" that I highly recommend. I love probability. My youngest sister is entering 9th grade in the fall and will be taking the accelerated course I taught this past year. My mom has asked me to work with her over the summer just to make sure she is 100% ready. I was able to reflect on the skills that my students needed this past to excel with the quick pace of Accelerated Coordinate Algebra/ Analytic Geometry A and decided to post what I plan on going through with my sister. She is SO excited to do math over the summer. She even rolls her eyes at me when I mention what is to come.
I have condensed the list to 3 major topics that every math student enrolling in the accelerated course should be 100% confident in. Topcis: 1) Solving one-step, two-step, and multiple-step linear equations 2) Graphing linear lines in various forms 3) Simplifying radicals with an index of two Kuta Software is awesome! The free trial has great worksheets that cover each topic and provide the answers. I am linking the worksheets I plan on having my sister work through. I will be there to help her but I also am showing her how to use tools like YouTube to watch quick tutorials on topics she wants more instruction for. Kuta Sheets by Topic 1) Solving one-step, two-step, and multiple-step linear equations One-Step Two-Step Multi-Step 2) Graphing linear lines in various forms Slope-Intercept Form Standard Form 3) Simplifying radicals with an index of two Worksheet 1, 2 This is just a start. I kept it to three major topics that I noticed that if my students where 100% in these areas they were able to focus on the new material and not be held up with much needed concepts. Happy Summer :) This is one of my favorite math music videos on YouTube. I believe it was completed for a class project but I honestly have NEVER seen a student produced video with such AMAZING quality (And I have done YouTube Video projects and they are great but not at this level). I find that videos over 2 minutes lose my student's interest but this one always captivates from beginning to end. Videos can help re-enforce or introduce a topic that has a lasting impact. I showed this to a Pre-Algebra class 2 years when I taught in Memphis and I had a former student contact me in January saying that she remembered the trigonometric ratios because of THIS video and it helped her in her Geometry class. Share it. Pass it on. This is awesome.  I typically hear less complaints (and a have higher homework completion rate) about an objective if one of two things happens: 1) The objective is easily understood by students 2) The students see the real-life application of the objective One way I show students the real-life application of an objective is through articles. I try to keep these articles to a front and back side of a paper and somewhat relevant and current. I also try to collect articles that I naturally read but I do resort to Google as well. As a math teacher, I do not feel 100% comfortable leading a whole class discussion comparable to what my students are exposed to in Literature but I can ask them what they think about the article and for the themes in the article. Some of my favorites from this year: 1) Parabolas in Basketball (I found this DURING March Madness and my parabola unit--it was fate!) 2) Zero being Even and Superstorm Sandy (A colleague sent this out) 3) Ben Franklin and Compound Interest (My students STILL talk about this--4 months later) It is amazing what you can find and tie into objectives. This is just the tip of the iceberg and I will continue to add articles that I use in my class. What do you use in your classroom? Vocabulary is essential in mathematics. In the past I have strayed away from it mainly because it is 'boring' and the past methods I have used have been ineffective. Through online research and collaboration with other teachers, I have been exposed to a variety of methods that work. "I have..., who has..." My favorite vocabulary strategy. The first 4 attached files are in reference to this activity. 14-16 students each have a different card. The student how has the card that states "I have the first card" reads that statement and then the "Who has...". The student who has the answer to the "Who has..." reads "I have..." and then their "Who has...". This continues till the last student reads "I have..." and then "The end." You can make it shorter or loner depending on if you want each student in your class to have a card. I have an average of 32 students in a class so I shot for half to have a card. I will time each class to see which class can finish in the least amount of time. This game typically takes about 2-5 minutes depending on the vocabulary. I will start a class with this and then end it with this as well to see how much time each class can shave off their first time. It is also great to use with known vocabulary objectives. I like to use this when teaching logarithms and exponents because it makes each student SAY the proper form. I will have a student at the front of the room time the activity, pass out/collect the cards, and they may write the "Who has..." part on the board. If someone reads the incorrect "I have..." I make the student holding the current "Who has..." read it again. This is to save on complete random guessing. Some classes like to have everyone with a card stand up and then sit down when they read their card. I sometimes tack on some extra points to the class with the fastest time. This has become common place in my teaching. I keep the initial print out as a key and make a copy of it on card stock that I then cut-out and hand out. I did not create the blank word document...I found it online. Fly Swatter You do need 2 fly swatters (try to the Dollar Tree) for this game and I think elementary teachers use this one a good bit but my older students enjoy it! Have the vocabulary show on the board in two columns with an overhead or projector. I then read a definition and the 2 students with the fly swatters try to the first student to "swat" the correct word with the fly swatter. It is entertaining to watch but you do need to be clear the fly swatters are only to tap the words and not others. (I do one class of Juniors that I do not do this activity with). You could even have teams and switch out the "swatter" for each word. This is quick and a great closing activity. Crossword Puzzles I see no value in word searches but I do see value in crossword puzzles (with no word blanks...that would defeat the purpose in my opinion). The only completely free site I have found is from Discover Education. It is not the best and I have not figured out a way to save a copy but it works! Taboo I love playing taboo and have always wanted to implement it for vocabulary. I plan on doing this in the future by giving each student a word and having this write the "taboo" words. This would be a great addition to any vocabulary day. I was thinking of using flashcards cut in half and adding the new words to the old words so that students were constantly reviewing previous vocabulary. I think groups of 8 (4 on each team) would be optional. Alright, I have convinced myself to do this. If I am spending a day on vocabulary I will do: 1st: "I have..., who has..." 2nd: Crossword 3rd: Fly Swatter 4th: "I have..., who has..." I would love to hear what other people are using. This is an area I want to continue to grow in!
 My freshman have started mastering the art of writing proofs. This is typically a difficult concept for students because they are used to making statements but stating the reason for each statement takes some getting used to. They were also having trouble understanding why they had to provide reasons for statements they felt where obvious. This is a common struggle for anyone writing proofs. Khan Academy has a great introductory video on geometry and Euclid's (Greek Mathematician.) For example, did you know that until recently that Euclid's Elements (13 volume Geometry Textbook) was the 2nd most produced book after the Bible? Isn't that crazy that a math textbook was second only to the Bible! The video also shows how Abraham Lincoln would read Euclid during his lawyer days when he needed to refresh on the importance of proving a point. This led to a comparison that if you where accused of murder do you want the lawyer that stands in the courtroom saying "Well, duh, this person is innocent" and then sits down or do you want the lawyer who proves to anyone in the room that you are not-guilty by showing evidence, cross-examining witnesses and brings in experts to represent you? I would love to purchase Euclid's masterpiece soon and contribute to its success and the lasting legacy of Euclid. |
Natalie Turbiville
Educator who loves math and working with students. Archives
May 2016
Categories
All
|
||||||||||||||||||||||||
 RSS Feed
RSS Feed
