|
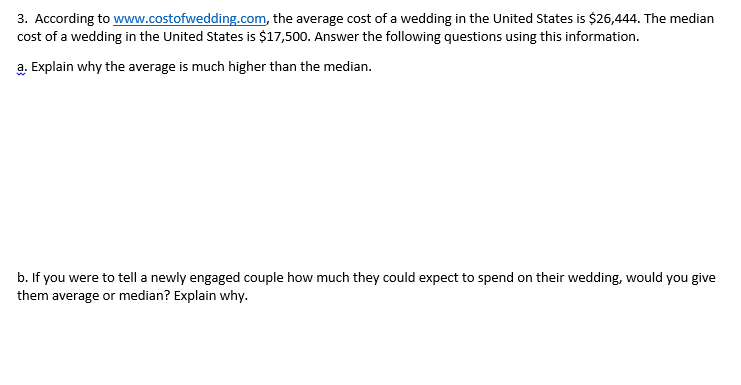
I love it when what is going on in life is relevant to what I am teaching. I am getting married this summer and am finding out just how expensive weddings are. Every site and article I read always seem to state the average cost of a wedding, however, I know from all the statistics classes I have taken that the mean is not always the best way to represent the typical value. My Advanced Pre-Algebra students are currently learning about the limits of basic statistics and the cost of a wedding in the United States is the perfect tie in for the debate of mean vs. median and the impact of outliers. On the quiz I gave my students Monday, I asked them the following... In part (a) I was looking for the use of the vocabulary of outlier and mentioning that there were expensive weddings that were bringing up the mean but not effecting the median. In part (b) I was looking for the students suggesting that the newly engaged couple be told the median since that value is not as influenced by the high outliers like the mean is. Below are some shots of my student's explanations. Before I returned graded quizzes, I had my students read Will Oremus' article: The Wedding Industry's Pricey Little Secret. Mr. Oremus does a great explaining that the averages are more than what most couples spend. He continues to point out that the sources who provided the public with the average (TheKnot.com, New York Post, etc...) typically exclude the poorest and most low-key couples from their samples simply because those couples are not on those sites or responding to the surveys. I especially enjoyed this section: Oremus goes on to explain why the median is not used as the statistic: Americans do not understand what the median is. TheKnot .com told Oremus that is does not publish the median along with the mean since they don't want to "confuse" people. When Oreums asked the editor in chief of TheKnot.com to expand more on why the median is not used, this was her response: She did not understand what the average was. Her reasoning is the typical error of most people-that the average tells you 50/50. The average serves as the balance of data, and not (usually) the indicator of the middle. That's the median. We had a great discussion as a class after they read they article. Thank you Will Oremus for a fantastic article that got my students talking about statistics and providing me some insight as I plan my wedding. Readers, I leave you with the closing remarks of Mr. Oremus: "There's nothing wrong with spending 28 G's in 24 hours if you've got the means. Just don't fool yourself into thinking that there's anything average about it" (emphasis added) (The file below is the word document I made from the article to print nicely. I printed 2 pages to 1, double sided.)
1 Comment
|
Natalie Turbiville
Educator who loves math and working with students. Archives
May 2016
Categories
All
|
||||||

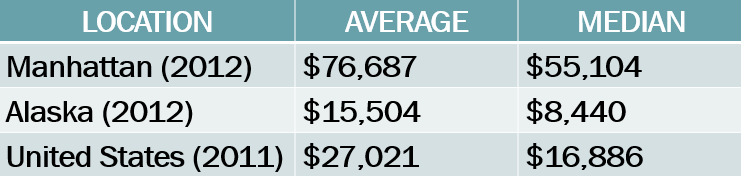


 RSS Feed
RSS Feed
